Nació el 31 de marzo de 1596 en La Haye, Turena (Francia) en el seno de una familia de funcionarios. Hijo de un consejero del Parlement de Bretaña. Su madre murió un mes después de su nacimiento, de la que heredó una fortuna que le permitió vivir con independencia económica. Con ocho años entró en la escuela jesuita de La Flèche en Anjou, donde permanecería hasta los 16 años. Junto a los típicos estudios clásicos Descartes estudió matemáticas y escolasticismo con el propósito de orientar la razón humana para comprender la doctrina cristiana. Estuvo influenciado por el Catolicismo. Al finalizar sus estudios en la escuela, se matriculó en Derecho en la Universidad de Poitiers, obteniendo la licenciatura en 1616. Sin embargo, nunca ejerció la profesión jurídica; en 1618 entró al servicio del príncipe Mauricio I de Nassau-Orange con la intención de seguir la carrera militar. Descartes sirvió en otros ejércitos pero su interés se centró siempre en los problemas de las matemáticas y la filosofía, a los que dedicó el resto de su vida.
Se trasladó a Italia, donde permaneció de 1623 a 1624 y marchó a Francia, donde residiría entre 1624 y 1628. En este periodo, se dedicó plenamente a la filosofía y a realizar experimentos de óptica. En 1628, tras vender sus propiedades en Francia, partió a Holanda, donde vivió en diferentes ciudades, Amsterdam, Deventer, Utrecht y Leiden. Fue por entonces cuando escribió Ensayos filosóficos, que fue publicada en 1637. Ésta está compuesta de cuatro partes: un ensayo sobre geometría, otro sobre óptica, un tercero sobre meteoros y el último, el Discurso del método, que describía sus especulaciones filosóficas. A éste le siguieron, entre otros ensayos, Meditaciones metafísicas (1641; revisado 1642) y Los principios de la filosofía, (1644). El último volumen fue dedicado a la princesa Elizabeth Stuart de Bohemia, que vivió en los Países Bajos y con la que mantenía una gran amistad.
Trató de aplicar a la filosofía los procedimientos racionales inductivos de la ciencia, y en concreto de las matemáticas. Antes de configurar su método, la filosofía había estado dominada por el método escolástico, que se basaba por completo en comparar y contrastar las opiniones de autoridades reconocidas. Rechazando este sistema, Descartes estableció: "En nuestra búsqueda del camino directo a la verdad, no deberíamos ocuparnos de objetos de los que no podamos lograr una certidumbre similar a las de las demostraciones de la aritmética y la geometría. Por este motivo dudó de todo hasta haber establecido las razones para creerla. Partió de la Primera verdad o Cogito, ergo sum, "Pienso, luego existo". A partir del principio de que la clara consciencia del pensamiento prueba su propia existencia, mantuvo la existencia de Dios. Dios, según la filosofía de Descartes, creó dos clases de sustancias que constituyen el todo de la realidad. Una clase era la sustancia pensante, o inteligencia, y la otra la sustancia extensa, o física. Su filosofía, también llamada cartesianismo, le llevó a elaborar explicaciones complejas y erróneas de diversos fenómenos físicos. Se aproximó a la teoría de Copérnico sobre el Universo, con su idea de un sistema de planetas giratorios moviéndose alrededor del Sol, renunció a esta teoría cuando fue considerada herética por la Iglesia católica. En su lugar ideó una doctrina de los vórtices o torbellinos de materia etérea, en la que el espacio estaba pleno de materia, en diversos estados, girando sobre el Sol.
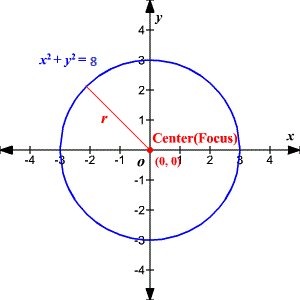
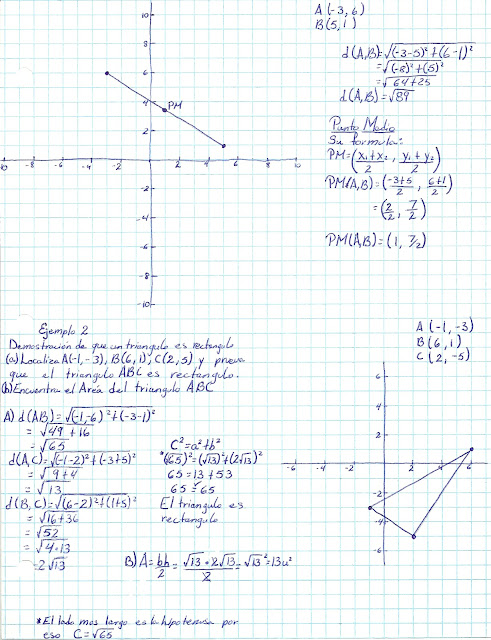
Su contribución más importante a las matemáticas fue la sistematización de la geometría analítica. Fue el primero que intentó clasificar las curvas conforme al tipo de ecuaciones que las producen, y contribuyó también a la elaboración de la teoría de las ecuaciones. Descartes fue el responsable de la utilización de las últimas letras del alfabeto para designar las cantidades desconocidas y las primeras letras para las conocidas. También inventó el método de los exponentes (como en x2) para indicar las potencias de los números. Además, formuló la regla, conocida como la ley cartesiana de los signos, para descifrar el número de raíces negativas y positivas de cualquier ecuación algebraica.
En 1649 Descartes fue invitado a la corte de Cristina de Suecia en Estocolmo para dar a la reina clases de filosofía. Todo parecía irle bien si Cristina no hubiera insistido en hacer que le enseñara filosofía a partir de las cinco de la mañana en un aposento grande y frío. Descartes era demasiado bien educado para quejarse de esta desagradable circunstancia, aunque siempre odiaba el frío y rara vez se levantaba antes del mediodía. Después de tres meses de estas espantosas clases antes del amanecer, enfermó de gravedad y murió el 11 de febrero de 1650 de una enfermedad respiratoria, que probablemente fue pulmonía. Diecisiete años más tarde, su cadáver volvió a París, donde fue sepultado.